Chapter 2: Statistical Learning

What is Statistical Learning

• Task: investigate the association between advertising and sales of a particular product

• Data: ad budget (in TV, Radio, and Newspaper) and sales for 200 markets

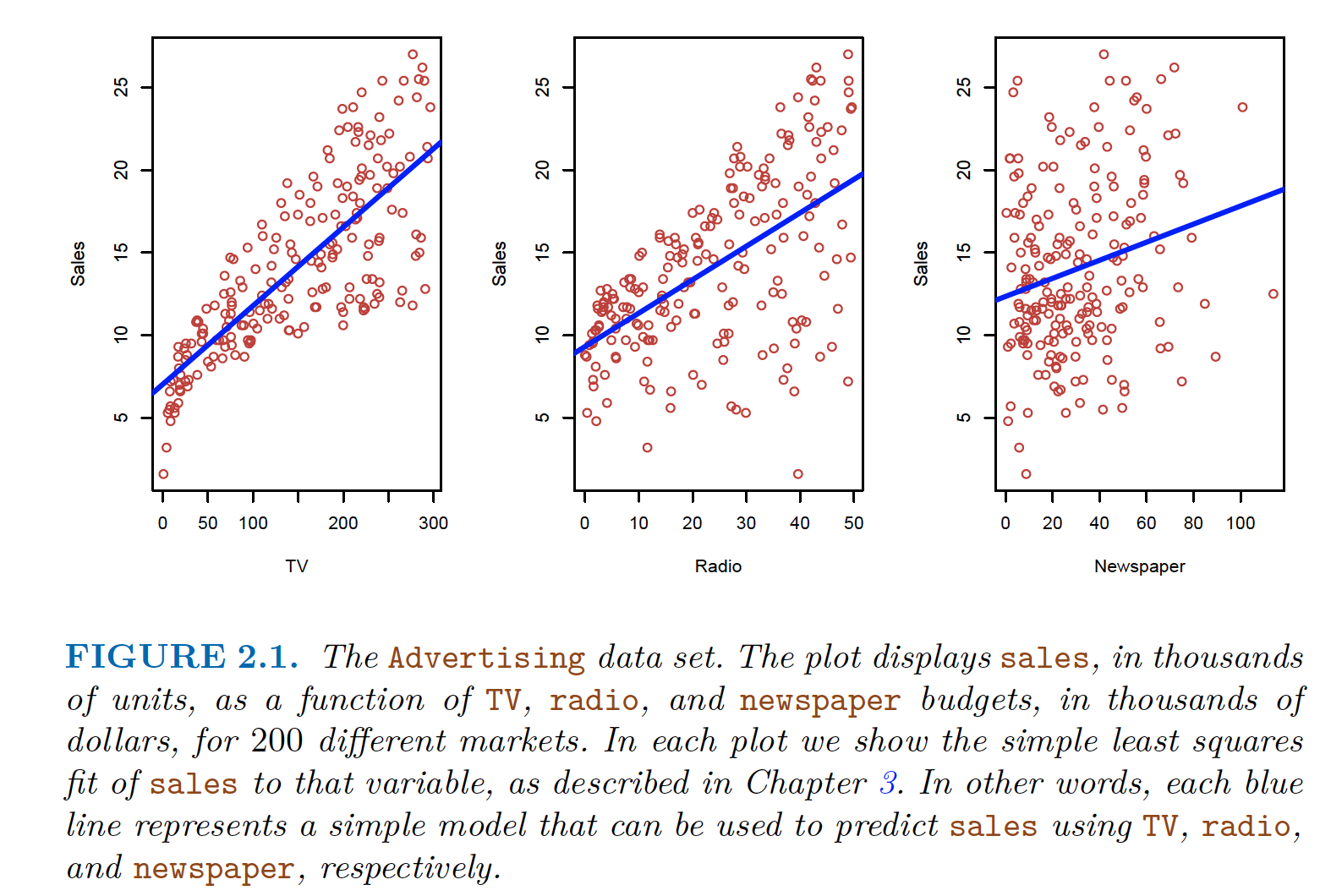
• Sales being predicted for TV, Radio, Newspaper

  Goal: Develop an accurate model that can be used to predict sales on the basis of the three media budgets.

• $X$: Predictor, independent variables, features, input variables

  • TV, Radio, Newspaper
  • $X = (X_1, X_2, …, X_p)$

• $Y$: Response, dependent variable

  • Sales

• Relationship:

  • \[Y = f(X) + \epsilon\]

  • $f$ is fixed, but an unknown function of $X_1, X_2, …, X_p$

  • $\epsilon$ is a random error term independent of $X$​ and mean zero

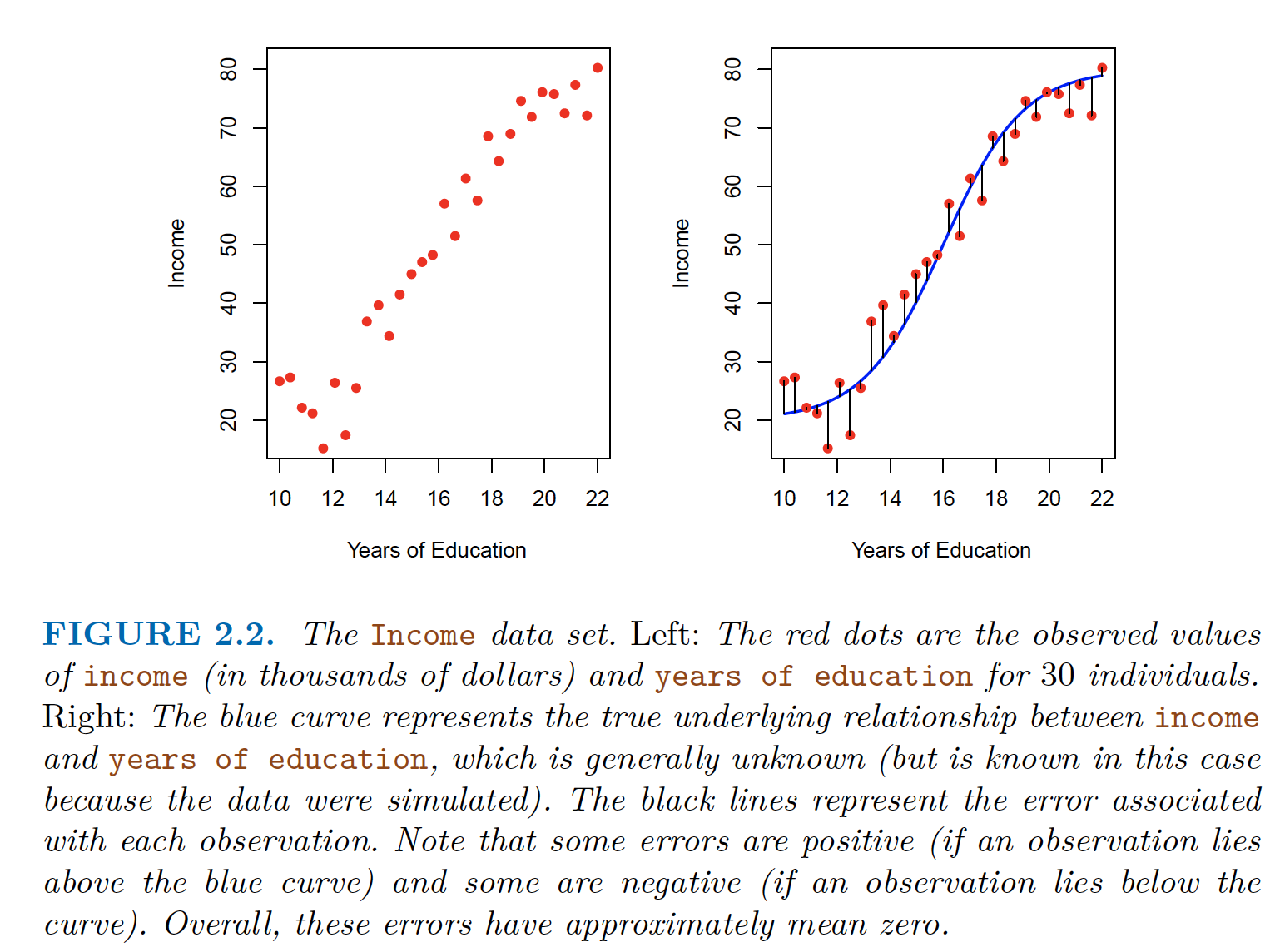
• Some errors are +ve and some -ve. Overall errors have approximately a mean zero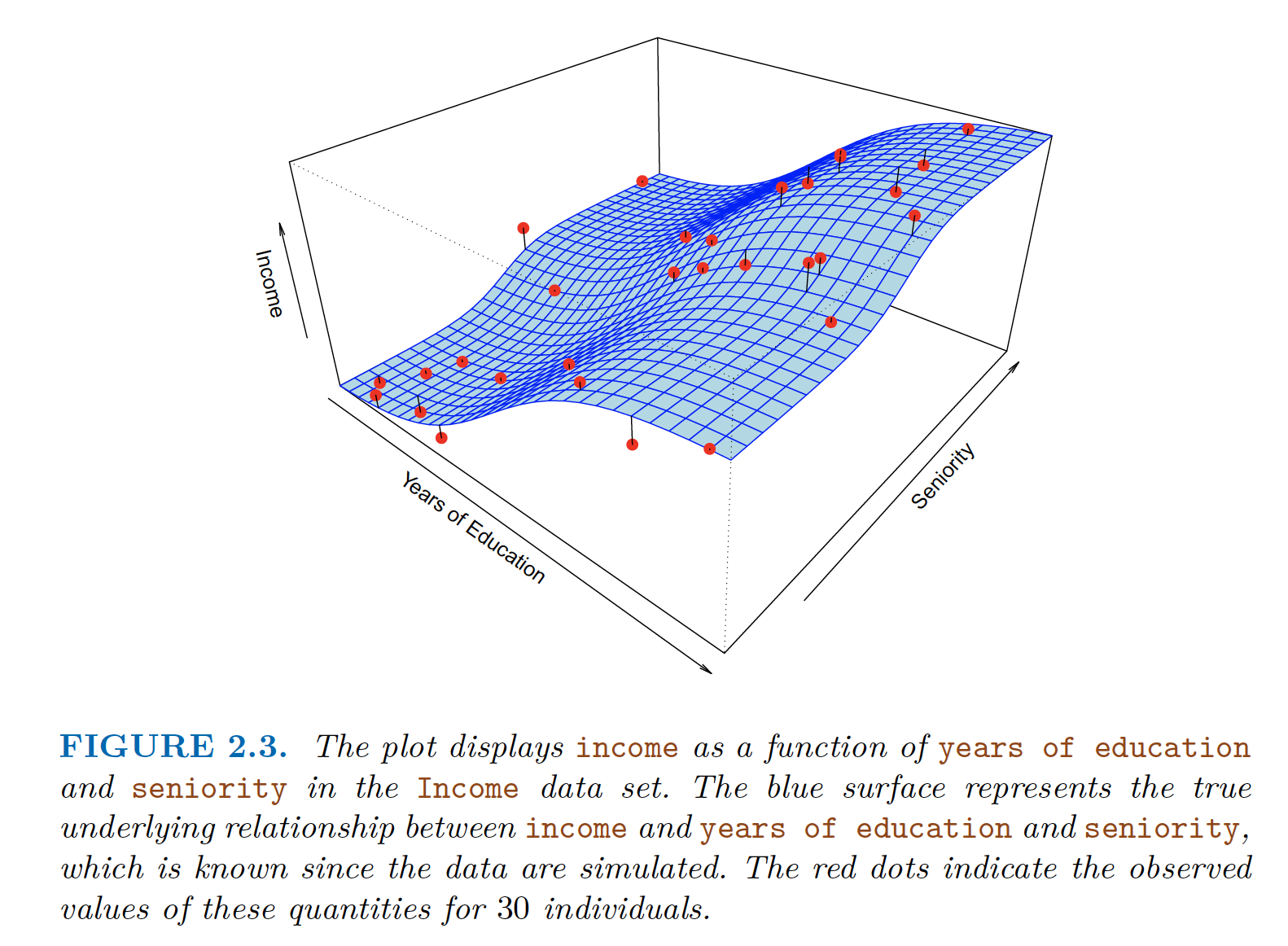

  Two Predictors and one response. Some errors are +ve and some -ve. Overall errors have approximately a mean zero

  In essence, statistical learning refers to a set of approaches for estimating $f$.

Why Estimate $f$

• Two Reasons

  • Prediction
  • Inference

• Prediction: $\hat{f}$ is black box

  • In many cases, $X$ is known and $Y$ is unknown. Since, $\epsilon$ averages to $0$

    • \[\hat{Y} = \hat{f}(X)\]

  • Accuracy of $\hat{Y}$ as a prediction of $Y$ depends on:

    • reducible error

      • since $\hat{f}$ is not a perfect estimate of $f$ but can be made perfect using a different technique

    • irreducible error

      • $Y$ is also a function of $\epsilon$. Further, $\epsilon$ may contain unmeasured variables that are useful in predicting $Y$
    • \[E(Y - \hat{Y})^2 &= E[f(X) + \epsilon - \hat{f}(X)]^2 \\ &= [f(X) - \hat{f}(X)]^2 + Var(\epsilon) \\ &= \text{Reducibile} + \text{irreducibile}\]

• Inference: $\hat{f}$ is not a black box

  • understanding association between $Y$ and $X_1, …, X_p$
  • Questions that can be answered:
    • Which predictors are associated with the response?
      • maybe a subset
    • What is the relationship between the response and each predictor?
      • maybe positive or opposite
    • Can the relationship between Y and each predictor be adequately summarized using a linear equation, or is the relationship more complicated?
  • Inference on Advertising data:
    • Which media are associated with sales?
    • Which media generate the biggest boost in sales? or
    • How large of an increase in sales is associated with a given increase in TV advertising?
  • Real Estate Data
    • How much extra will a house with a river view be worth?
      • Inference
    • Is this house under or over-valued?
      • Prediction
  • Goal: Prediction or Inference or Combination
    • Linear model: simple and interpretable inference but less accurate prediction
    • Non-linear Approaches: More accurate predictions at the cost of inference and less interpretable model

How do we estimate $f$

• Using Training Data

  • ${(x_1, y_1), (x_2, y_2), . . . , (x_n, y_n)}$, where $xi = (x_{i1}, x_{i2}, . . . ,x_{ip})^T$
  • Find $\hat{f}$ such that $Y \approx \hat{f}(X)$
  • The method can be Parametric or Non-parametric

• Parametric Methods

  • Two steps approach

    • Step 1: make assumptions about the functional form, e.g. shape

      • e.g. Linear Model: $f$ is linear in $X$

      • \[f(X) = \beta_0 + \beta_1X_1 + \beta_2X_2 + · · · + \beta_pX_p \label{eq:lm}\]
        • Now, instead of estimating entirely arbitrary p-dimensional function f(X), one only needs to estimate the $p + 1$ coefficients $\beta_0, \beta_1, . . . , \beta_p$.

    • Step 2: Train the model on the data

      • Linear model in Equation $\eqref{eq:lm}$ can be trained by (ordinary) least squares

  • Problem is to reduced to find a set of parameters => parametric

  • However, the model may not match the true form of $f$. We can choose flexible model with greater number of parameters. However, this can overfit that means it can fit to noise or errors too closely.

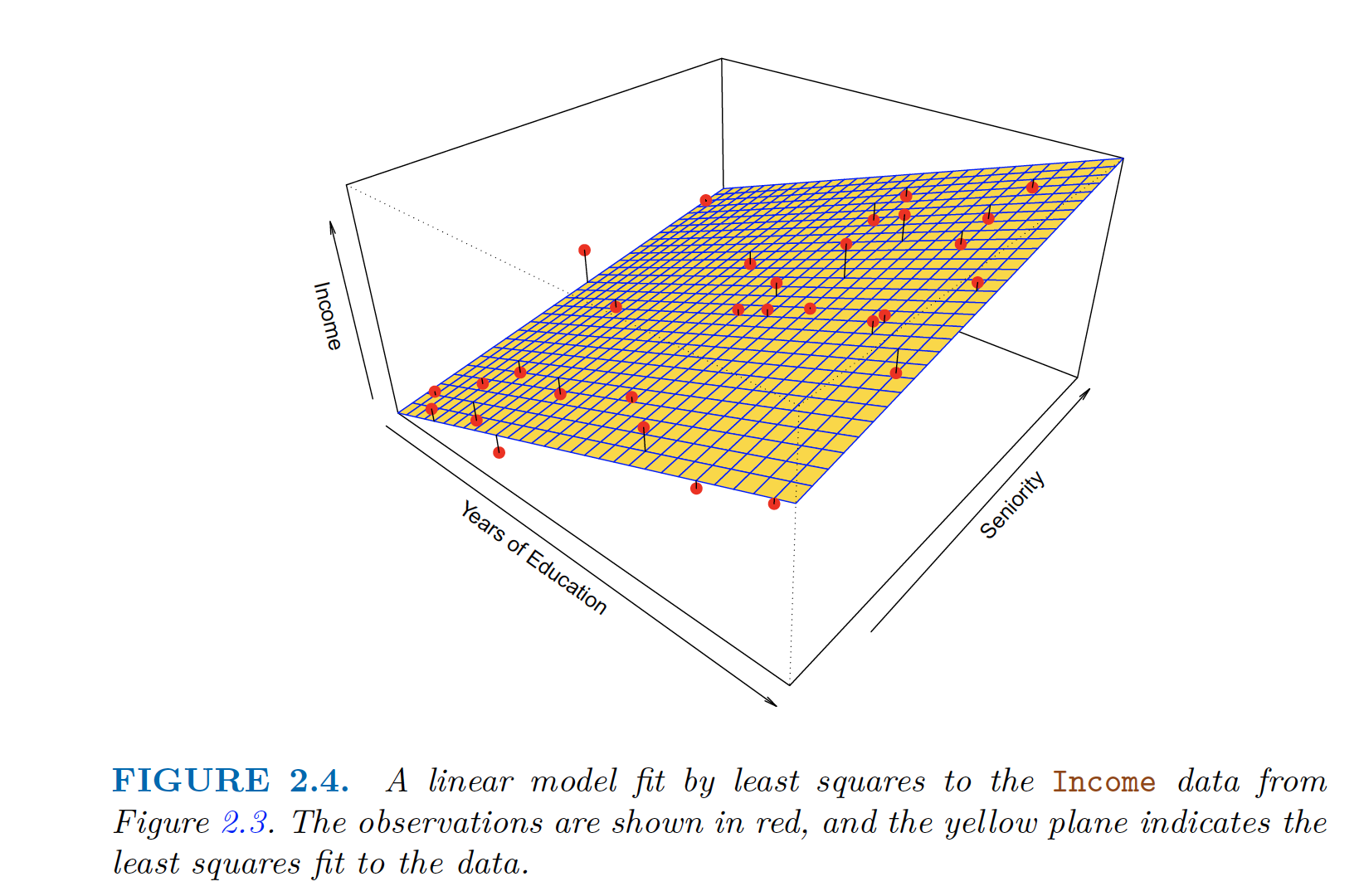
  • Parametric Approach applied to Income Data

    $income \approx \beta_0 + \beta_1 \times education + \beta_2 \times seniority$

  • True data as in figure 2.3 has some curvature while 2.4 doesn’t capture that. However it still captures the relationship.

• Non-parametric Methods

  • No assumption about $f$

    • However, a very large number of observations (far more than is typically needed for a parametric approach) is required in order to obtain an accurate estimate for $f$.

  • For example, thin-plate spline

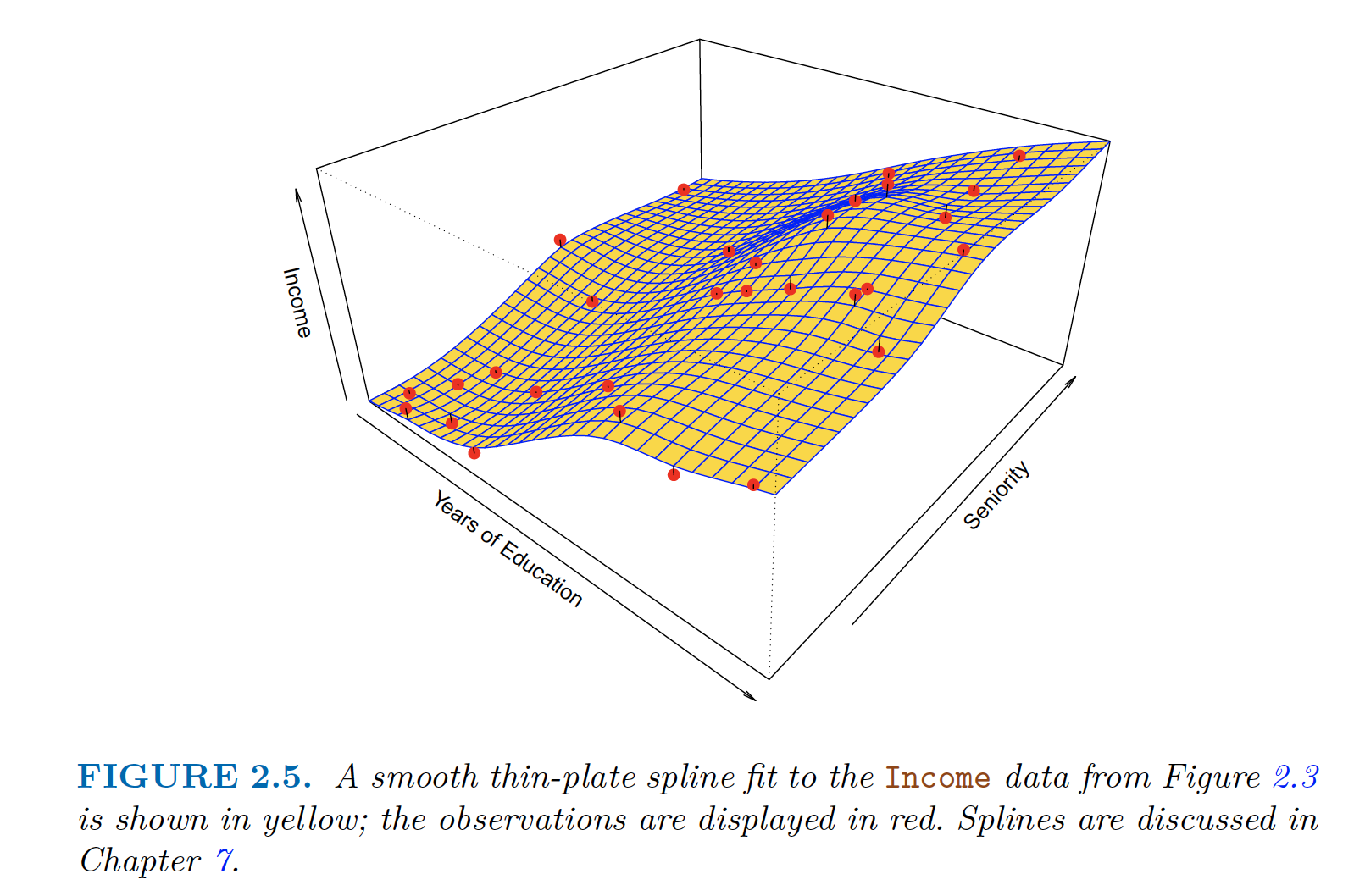
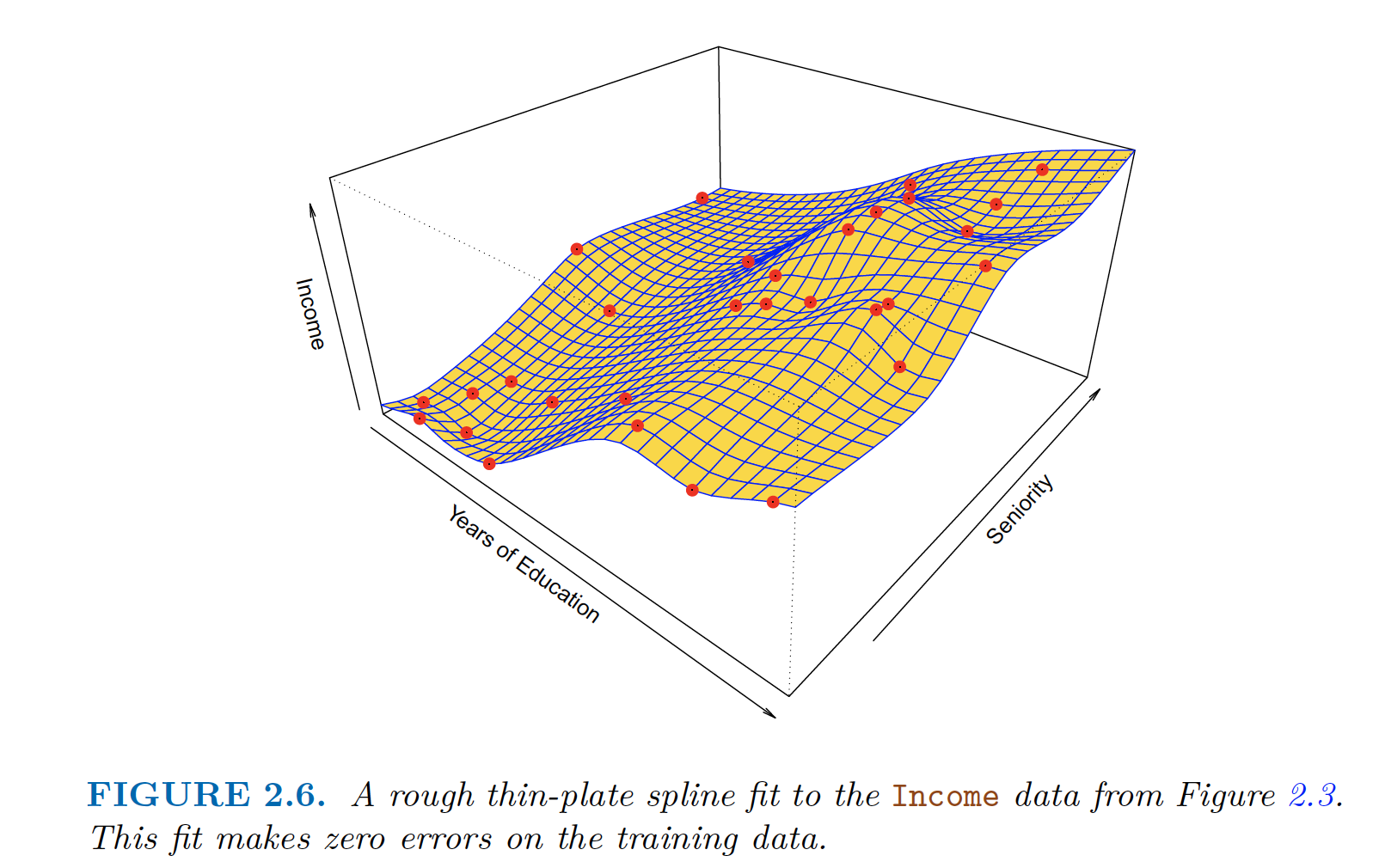
  • Thin-plate Spline, need to select level of smoothness	Thin-plate Spline, with low level of smoothness (zero error) - overfitting

The Trade-Off Between Prediction Accuracy and Model Interpretability

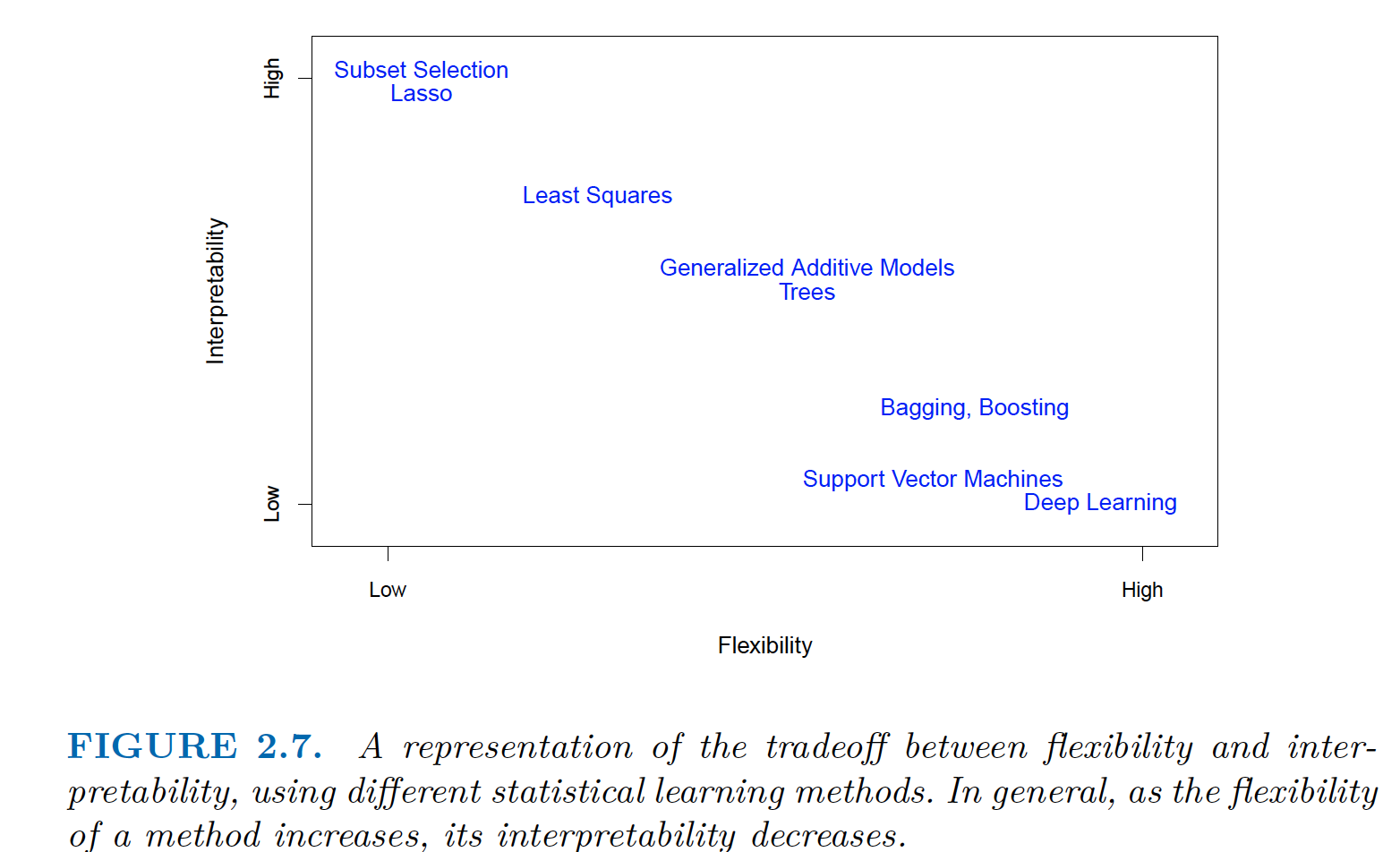Low Flexibility => High Interpretability and High Flexibility => Low Interpretability

Supervised Versus Unsupervised Learning

Regression Versus Classification Problems

Assessing Model Accuracy

Measuring the Quality of Fit

• Compute for test data

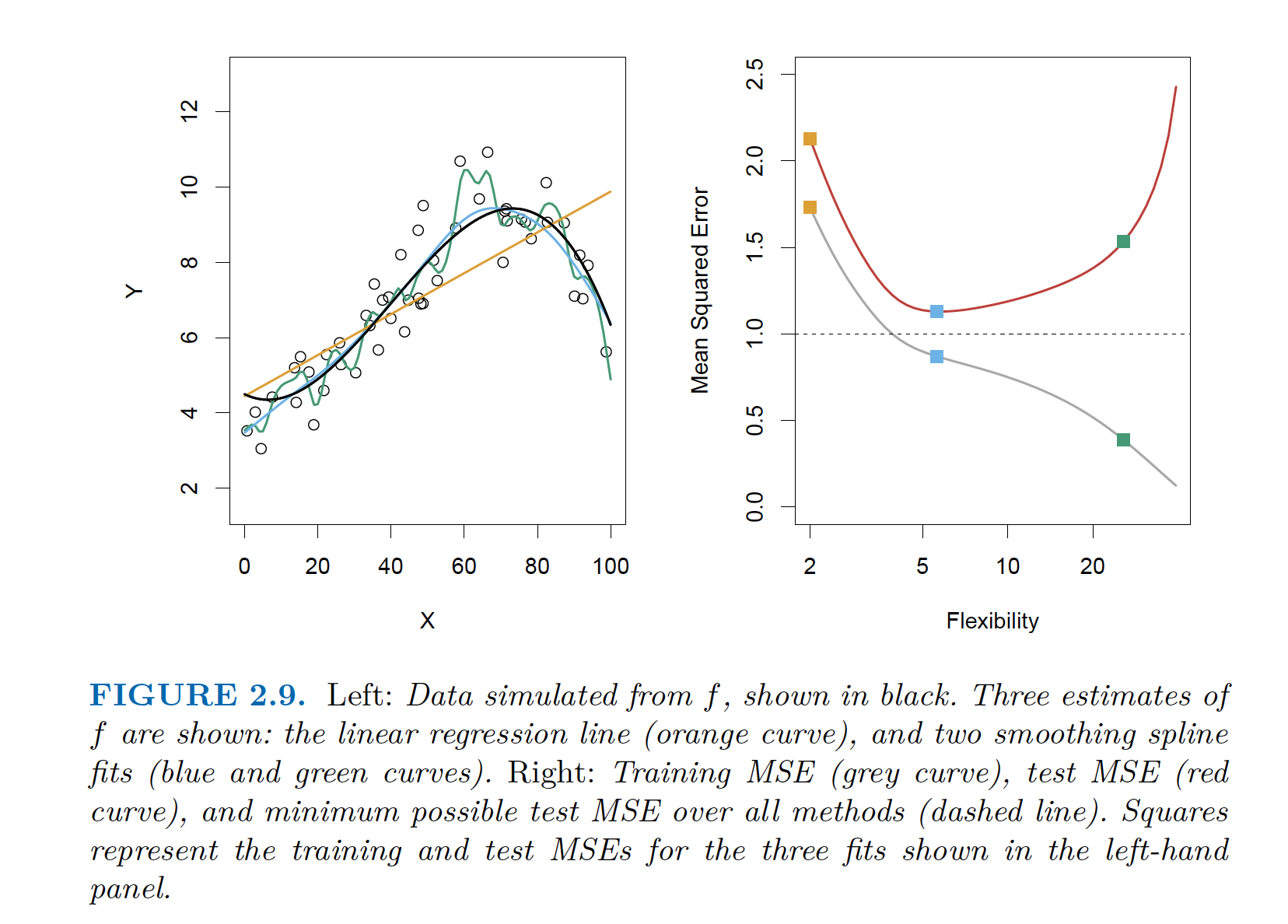Left: Actual (Black), Linear Regression (orange), Split fit 1(blue), Split fit 2(green) Right: Train and Test Error for Linear Regression (orange), Split fit 1(blue), Split fit 2(green)

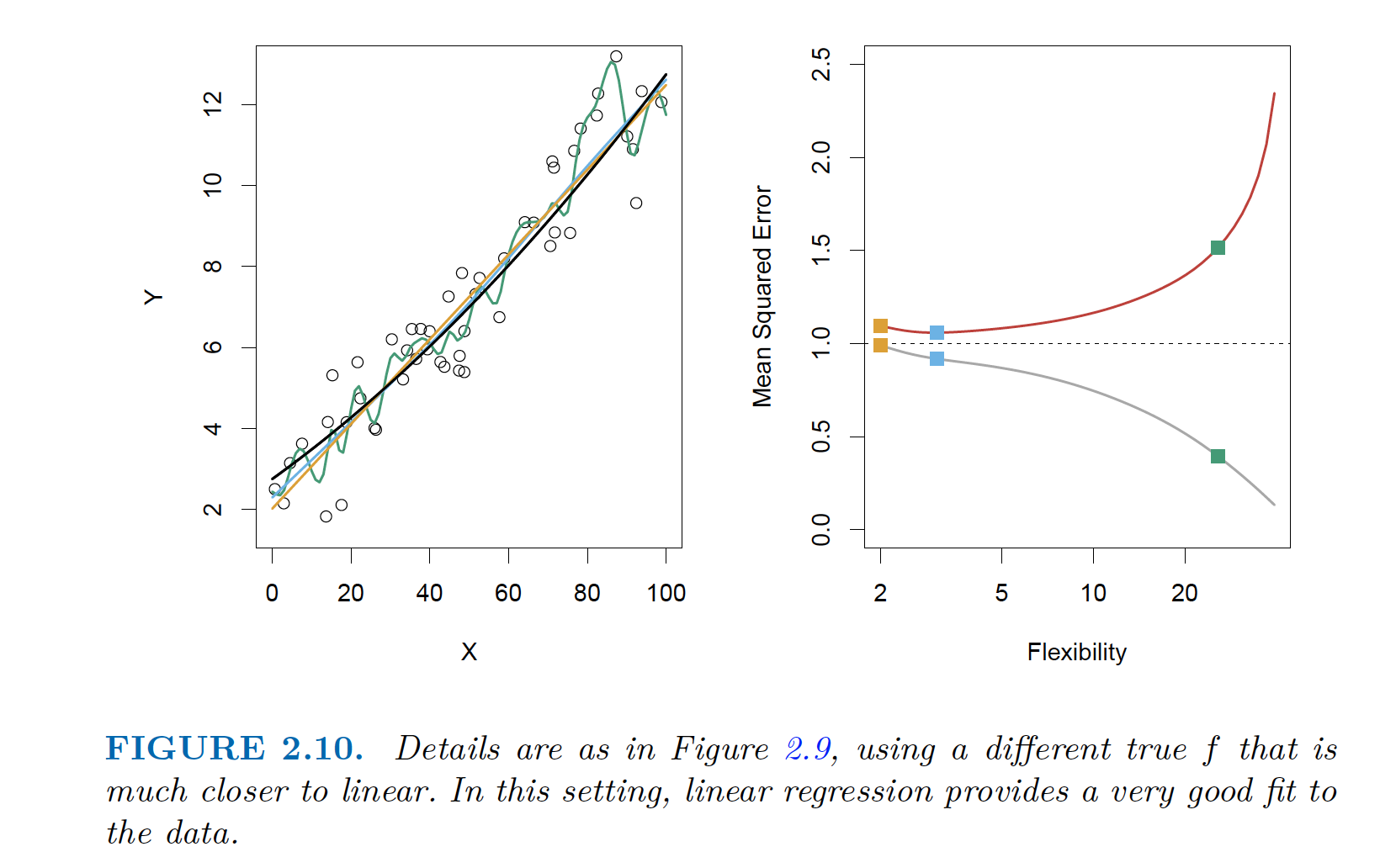
Another example: Linear Regression has both errors small

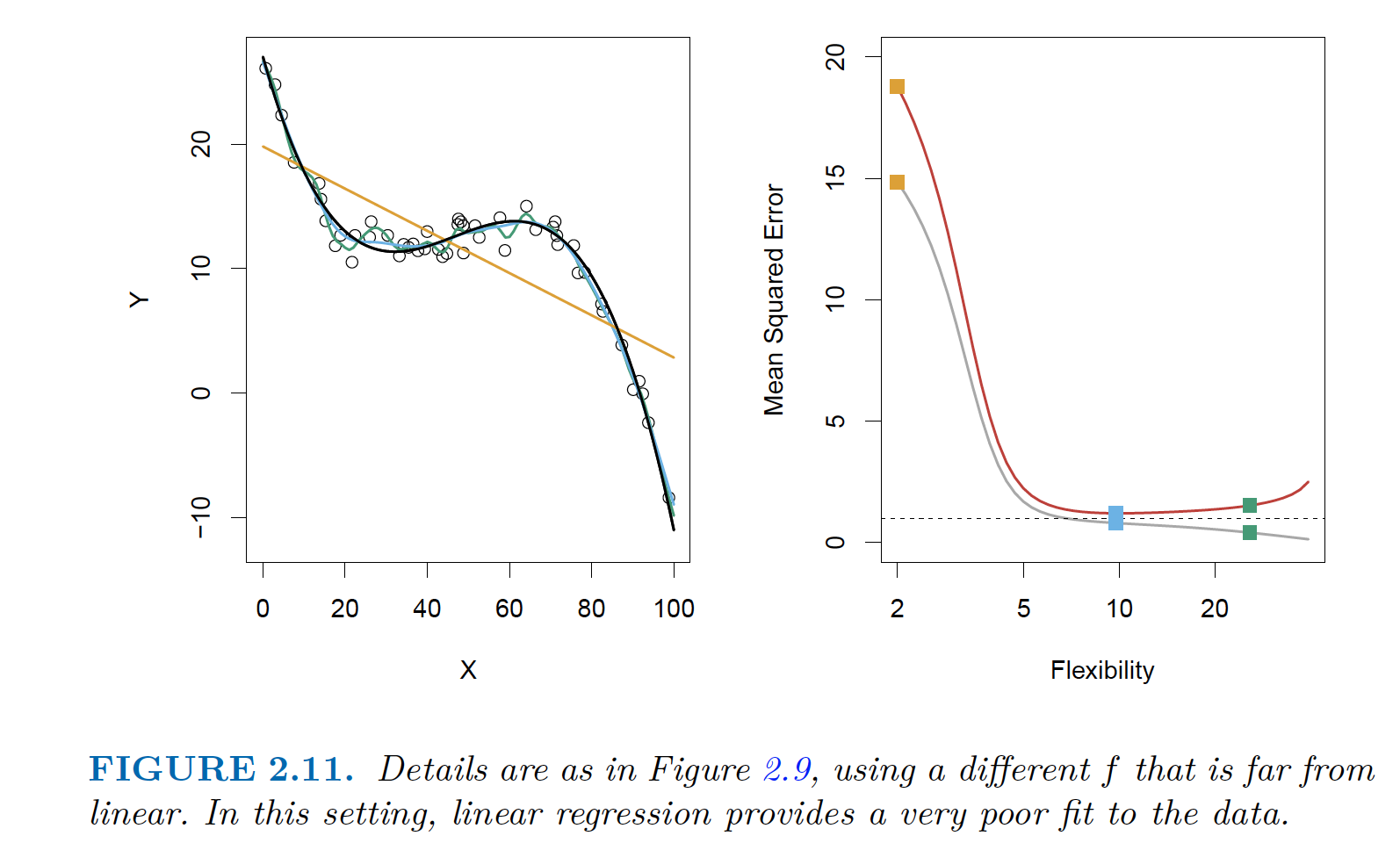
Linear Regression is poor. Both errors are high.

The Bias-Variance Trade-Off

• To minimize the test MSE, we need to minimize Var and Bias. Variance is non-negative and Squared Bias is also non-negative. Thus minimum expected test is $Var(\epsilon)$, irreducible term.
• Variance
  • refers to the amount by which $\hat{f}$ would change if we estimated it using a different training data set.
  • Ideally, $\hat{f}{training_data_1} \approx \hat{f}{training_data_2}$
  • High Var
    • small changes in training data => large changes in $\hat{f}$
    • In general, more flexible statistical methods => higher variance.
• Bias
  • refers to the error that is introduced by approximating a real-life problem e.g. assumption that there is linear relationship. Irrespective of the amount of training data, there will always be error.
• Trade-off
  • Linear Regression can have more bias. Thus, we need more flexible methods to accurately represent the data but that can lead to high variance