This lesson covers PyTorch Tutorial, https://pytorch.org/tutorials/beginner/basics/intro.html

Automatic Differentiation with torch.autograd

• When training neural networks, the most frequently used algorithm is back propagation
• parameters (model weights) are adjusted according to the gradient of the loss function with respect to the given parameter
• To compute those gradients, PyTorch has a built-in differentiation engine called torch.autograd
• It supports automatic computation of gradient for any computational graph

topic = "pytorch"
lesson = 6

from n import *
home, models_path = get_project_dir("FashionMNIST")
print(home)

/home/naneja/datasets/n/FashionMNIST

import torch
import random
import numpy as np

seed = 0


os.environ['PYTHONHASHSEED'] = str(seed)

# Torch RNG
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)

torch.use_deterministic_algorithms(True)

# Python RNG
np.random.seed(seed)
random.seed(seed)

x = torch.ones(5)  # input tensor
print_("Input Tensor", x)

y = torch.zeros(3)  # expected output
print_("Expected Output ", y)

torch.manual_seed(seed)
w = torch.randn(5, 3, requires_grad=True)
print_("Initial w ", w)

b = torch.randn(3, requires_grad=True)
print_("Bias ", b)

z = torch.matmul(x, w)+b
print_("logits ", z)

loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)
print_(f"loss={loss:.4f}")

Input Tensor

tensor([1., 1., 1., 1., 1.])

Expected Output

tensor([0., 0., 0.])

Initial w

tensor([[ 1.5410, -0.2934, -2.1788],
        [ 0.5684, -1.0845, -1.3986],
        [ 0.4033,  0.8380, -0.7193],
        [-0.4033, -0.5966,  0.1820],
        [-0.8567,  1.1006, -1.0712]], requires_grad=True)

Bias

tensor([ 0.1227, -0.5663,  0.3731], requires_grad=True)

logits

tensor([ 1.3755, -0.6023, -4.8127], grad_fn=<AddBackward0>)

loss = 0.6819

Tensors, Functions and Computational graph

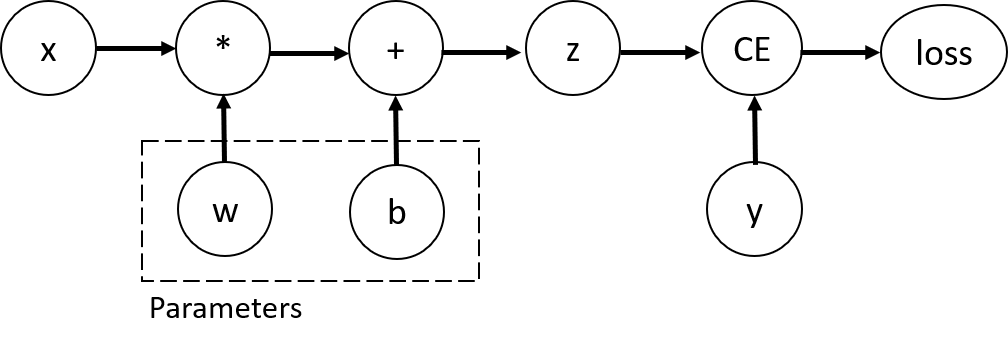
• w and b are parameters, which we need to optimize

• compute the gradients of loss function with respect to those variables

• set the requires_grad property of those tensors
  • set the value of requires_grad when creating a tensor or later
  • by using x.requires_grad_(True) method
• A function that we apply to tensors to construct computational graph is in fact an object of class Function
• This object knows how to compute the function in the forward direction, and also how to compute its derivative during the backward propagation step
• A reference to the backward propagation function is stored in grad_fn property of a tensor

print_(f"Gradient function for z = {z.grad_fn}")
print_(f"Gradient function for loss = {loss.grad_fn}")

Gradient function for z = <AddBackward0 object at 0x7f65d6afe320>

Gradient function for loss = <BinaryCrossEntropyWithLogitsBackward0 object at 0x7f66869c5c60>

Computing Gradients

• To optimize weights of parameters in the neural network, we need to compute the derivatives of our loss function with respect to parameters
• $\frac{\partial loss}{\partial w}$ and $\frac{\partial loss}{\partial b}$, under some fixed values of x and y
• To compute those derivatives, we call loss.backward(), and then retrieve the values from w.grad and b.grad

loss.backward()
print(w.grad)
print(b.grad)

tensor([[0.2661, 0.1179, 0.0027],
        [0.2661, 0.1179, 0.0027],
        [0.2661, 0.1179, 0.0027],
        [0.2661, 0.1179, 0.0027],
        [0.2661, 0.1179, 0.0027]])
tensor([0.2661, 0.1179, 0.0027])

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output

torch.manual_seed(seed)
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)

z = torch.matmul(x, w)+b

loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

loss.backward()

print_(f"w.grad")
print(w.grad)

print_(f"b.grad")
print(b.grad)

w.grad

tensor([[0.2661, 0.1179, 0.0027],
        [0.2661, 0.1179, 0.0027],
        [0.2661, 0.1179, 0.0027],
        [0.2661, 0.1179, 0.0027],
        [0.2661, 0.1179, 0.0027]])

b.grad

tensor([0.2661, 0.1179, 0.0027])

• We can only obtain the grad properties for the leaf nodes of the computational graph, which have requires_grad property set to True.

• For all other nodes in our graph, gradients will not be available.

• We can only perform gradient calculations using backward once on a given graph, for performance reasons.

• If we need to do several backward calls on the same graph, we need to pass retain_graph=True to the backward call.

Disabling Gradient Tracking

• By default, all tensors with requires_grad=True are tracking their computational history and support gradient computation.

• We can stop tracking computations by surrounding our computation code with torch.no_grad() block

• Reasons to disable gradient tracking

  • To mark some parameters in your neural network as frozen parameters. This is a very common scenario for finetuning a pretrained network
  • To speed up computations when you are only doing forward pass, because computations on tensors that do not track gradients would be more efficient

z = torch.matmul(x, w)+b
print_(f"z.requires_grad: {z.requires_grad}")

with torch.no_grad():
    z = torch.matmul(x, w)+b
print_(f"z.requires_grad: {z.requires_grad}")

z.requires_grad: True

z.requires_grad: False

# Another way to disable gradient
z = torch.matmul(x, w)+b
print_(f"z.requires_grad: {z.requires_grad}")

z_det = z.detach()
print_(f"z.requires_grad: {z.requires_grad}")

z.requires_grad: True

z.requires_grad: True

More on Computational Graphs